Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
Tags
- 네트워크
- 정보처리기사개정
- 정보
- array
- 취업사실신고
- 튜터링
- 실업인정인터넷신청
- C++
- 생애첫계약
- 막대기자르기
- 자료구조
- 후니의쉽게쓴시스코라우팅
- 실업급여
- 후니의쉽게쓴시스코네트워킹
- 회사폐업
- leetcode
- 코딩테스트
- 프로그래머스
- 자취준비
- 모여봐요동물의숲
- 캡쳐링
- 순열
- IT기초
- 사회초년생
- 알고리즘
- 전화영어
- HeadFirstDesignPatterns
- 동적계획법
- 부분합알고리즘
- 청년내일채움공제
Archives
- Today
- Total
따봉도치야 고마워
배열 최대 연속 부분합 4가지 알고리즘 본문
문제
https://www.acmicpc.net/problem/1912
1912번: 연속합
첫째 줄에 정수 n(1 ≤ n ≤ 100,000)이 주어지고 둘째 줄에는 n개의 정수로 이루어진 수열이 주어진다. 수는 -1,000보다 크거나 같고, 1,000보다 작거나 같은 정수이다.
www.acmicpc.net
연속된 배열에서 합이 최대가 되는 연속 부분 합을 찾아라
ex)
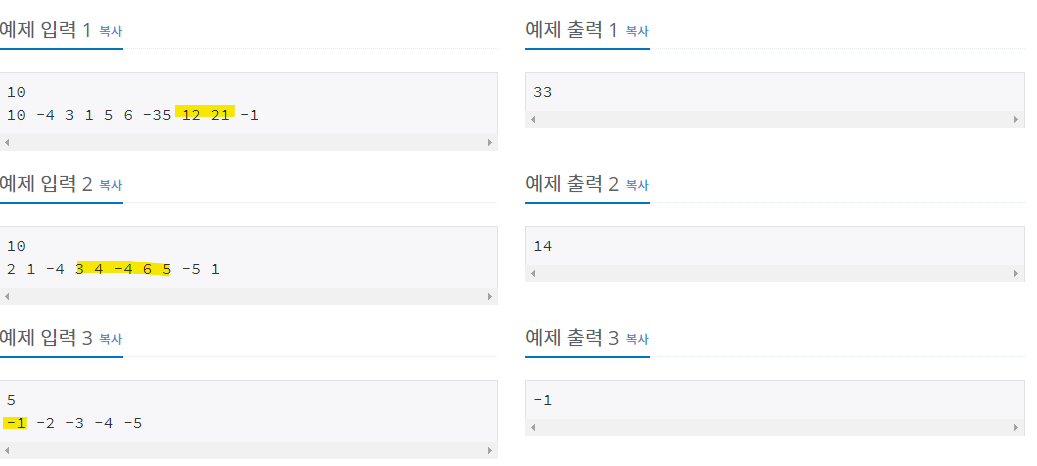
풀이
1.완전탐색
2.부분합 배열 사용
3.분할정복
4.동적계획법
- 일단 f(i) = i를 끝으로 하는 배열의 최대합으로 생각하면
- f(i) = max(0, f(i-1)) + 현재 원소값이 된다.
무슨 소리냐면 이전까지 더해온 합이 음수라면, 현재 원소값을 더한 값 < 현재 원소값 이 확정이기 때문에 0으로 초기화 해준다.
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
int main()
{
int n;
scanf("%d", &n);
vector<int> arr(n, 0);
vector<int> cache(n, 0);
for (int i = 0; i < n; i++) {
scanf("%d", &arr[i]);
}
//초기화
cache[0] = arr[0];
int ret = cache[0];
for (int i = 1; i < n; i++) {
cache[i] = max(0, cache[i-1]) + arr[i];
if(cache[i] > ret){
ret = cache[i];
}
}
printf("%d\n", ret);
return 0;
}
// cache[i] = max(0, cache[i-1]) + arr[i]; 이부분을 cache[i] = max(cache[i-1]+arr[i], arr[i]); 이렇게 수정해도 될듯!
---
일단은 동적계획법만 정리했고 추후 수정할 포스팅입니다.
'프로그래밍 > 알고리즘' 카테고리의 다른 글
| [프로그래머스] 해시 : 전화번호 목록 (0) | 2020.05.20 |
|---|---|
| [프로그래머스] 해시 : 완주하지 못한 선수 (0) | 2020.05.19 |
| [DP] 2*N 타일링 (0) | 2020.03.31 |
| 동적 계획법(Dynamic Programming) 과 탐욕법(Greedy Algorithm) (0) | 2020.03.26 |
| [프로그래머스] 기능개발 (0) | 2020.03.24 |
Comments


